ParaView/Surface LIC Implementation: Difference between revisions
No edit summary |
No edit summary |
||
| Line 21: | Line 21: | ||
= Controls = | |||
== Noise Texture == | |||
== High-Pass Filter == | |||
== Anti-Aliasing == | |||
== | == Gray Scale Color Normalization == | ||
== Scalar Blending == | |||
Latest revision as of 01:14, 23 October 2012
This page describes implementation details of ParaView's Surface LIC Representation. The Surface LIC Representation is provided as a ParaView plugin.
Implementation Details
Algorithm
The current implementation is based on a combination of the following two algorithms:
| Brian Cabral and Leith Casey Leedom. 1993. Imaging vector fields using line integral convolution. In Proceedings of the 20th annual conference on Computer graphics and interactive techniques (SIGGRAPH '93). ACM, New York, NY, USA, 263-270. DOI=10.1145/166117.166151 http://doi.acm.org/10.1145/166117.166151 |
| Robert S. Laramee, Bruno Jobard, and Helwig Hauser. 2003. Image Space Based Visualization of Unsteady Flow on Surfaces. In Proceedings of the 14th IEEE Visualization 2003 (VIS'03) (VIS '03). IEEE Computer Society, Washington, DC, USA, 18-. DOI=10.1109/VISUAL.2003.1250364 http://dx.doi.org/10.1109/VISUAL.2003.1250364 |
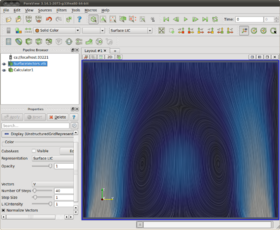
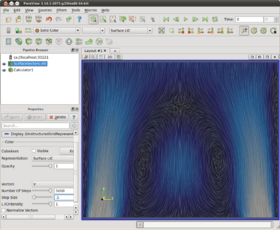
Vector Normalization
One of the differences between the Cabral's algorithm and Laramee's algorithm is that Cabral's normalizes the vector field during integration. In ParaView one may select between normalized and un-normalized vectors during integration. When vector normalization is enabled(the default) the input vector field is normalized during integration, and each integration occurs over the same arc length. This tends to make all regions of flow look similar despite any differences in flow strength. When vector normalization is disabled each integration occurs over an arc length proportional to the field magnitude, which tends to visually retain relationships between strong and weak regions of flow. Both are valid approaches but the input parameters used to produce good results will be quite different for each. It's easier to get consistently good results across many datasets when normalizing the vector field, thus this should be one's first choice. The following two screen shots illustrate the difference between normalizing and not.
Surface LIC with vector field normalization enabled
Surface LIC with vector field normalization disabled
